Optimaalset ACS-i peetakse mõnes mõttes parimaks süsteemiks. Optimaalsuse kriteeriumid võivad olla erinevad ja sõltuvad lahendatavast probleemist. Kõige tavalisemad optimaalsuse kriteeriumid on:
1) ACS-i täpsus muutuva mõju korral,
2) üleminekuaeg,
3) Kasumlikkus;
Performance;
Integraalsed kriteeriumid.
Praeguseks on suurim areng süsteemide optimaalsuse teoorias saanud 2 valdkonda:
1) süsteemide liikumise optimaalse juhtimise teooria täieliku teabega objekti ja häirete kohta;
Optimaalse juhtimise teooriad juhuslike häirete korral.
Optimaalse kontrolli rakendamiseks on vaja:
Määrake juhtimise eesmärk. Eesmärki väljendatakse kas eesmärgifunktsiooni või optimeerimiskriteeriumiga.
Sihtfunktsioon ehk optimeerimiskriteerium võimaldab leida mis tahes lahenduse kvantitatiivse efekti.
Valige analüüsimiseks mudel ja määrake otsuse tõhusus.
Uurida kõiki objekti toimimiskeskkonna olekuid, mis mõjutavad juhtimisprotsessi minevikku, olevikku ja tulevikku.
Optimaalse juhtimise ülesande lahendamisel kasutatakse variatsiooniarvutuse meetodeid, maksimumprintsiipe, aga ka dünaamilist ja matemaatilist programmeerimist.
Üldjuhul optimaalse kontrolliprobleemi saab sõnastada järgmiselt:
1) Juhtimise eesmärk, mis on matemaatiliselt esindatud mõne funktsionaalse või juhtimiskriteeriumi kujul
2) Süsteemivõrrandid - need esitatakse tavaliselt olekuvõrrandite kujul
3) Piirvõrrandi süsteem alg- ja lõppajal.
4) piirangute süsteem, millele olekumuutujad ja võrrandid peavad vastama.
Vajalik leidmiseks:
Juhtvektor, mille juures kontrolleesmärgi kriteeriumil on ekstreemum (max või min).
Tuleb märkida, et mõnel juhul ei pruugi optimaalne kontroll olemas olla ja seda ei saa ilma probleemi lahendamiseta hinnata. Optimaalse kontrolli leidmise probleemi lahendus on mitmetähenduslik, s.t. iga leitud lahendus annab lokaalse optimumi. Kui kõik lokaalsed optimumid on leitud, saab sel juhul tuvastada globaalse optimumi. Leitud globaalne optimum on optimaalse juhtimisprobleemi lahendus.
Integreeritud kvaliteedikriteeriumid:
Optimaalne jõudlus
Funktsionaalsusel on vorm

Optimaalne jõudlus
Optimaalsuse kriteeriumiks on pöördenurk teatud aja jooksul t ja funktsionaal on kujul

Optimaalne ökonoomsus
Optimaalsuse kriteeriumiks on energiakulu teatud aja jooksul ja funktsionaalsel on vorm

28. Regulaatorite analüütiline disain. Probleemi sõnastamine.
Lineaarsetes automaatjuhtimissüsteemides siirdekvaliteedi uurimisel võeti kasutusele väljavalgunud integraalsed kvaliteedikriteeriumid, mille abil hinnati siirdeprotsessi lõpmatu ajavahemiku jooksul. Arvestades terviklikke kvaliteedikriteeriume, veendusime, et need kriteeriumid võimaldavad meil määrata kontrolleri parameetreid, kui selle struktuur on antud. Võib püstitada üldisema probleemi: leida reguleerimisseadus - analüütiline funktsioon, mis ühendab juhtimiskoordinaadi ja juhtimistoimingut, pakkudes samal ajal integraalsele kvaliteedikriteeriumile min. Sellist regulaatori diferentsiaalvõrrandi optimaalset ülesehitust nimetatakse regulaatorite analüütiliseks disainiks. Lahendusmeetodite ja probleemi sõnastuse poolest sarnaneb see probleem optimaalsete kontrolliprobleemidega.

See on variatsiooniprobleem, kus X-i ja U-d ühendavat funktsiooni otsitakse äärmuslikuna.
Analüütilise projekteerimise ülesandeks on leida juhtimisseadus, mis tehase võrrandeid ja piirtingimusi arvestades annaks süsteemi ruutviga iseloomustava ja selle stabiilsust tagava integraalini min.
Kontrollerite optimaalse disaini probleemi avaldus.
Reguleerimise objekt määratakse diferentsiaalvõrrandite abil, mis operaatori kujul vastab ülekandefunktsiooni Wop(S) (või W(S)) omistamisele.
Arvatakse, et välised häired süsteemile ei mõju ja üleminekuprotsess toimub algtingimuste muutumisel.

X  = y 0 – y – mittevastavus
= y 0 – y – mittevastavus
Stabiilses lineaarses ACS-is peaksid siirdeprotsessi tulemusena kõik koordinaatfunktsioonid kalduma 0-le. x 1 () = x 2 () = ... xn () = U () = 0 (2) )
Optimaalsuse kriteeriumiks valime vormi integraali
(3), kus V on positiivne kindel ruutvorm.
 Need. kui asendame V väärtusega (3), on see süsteemi ruutviga.
Need. kui asendame V väärtusega (3), on see süsteemi ruutviga.
Liige U 2 punktis (4) iseloomustab kontrolliprotsessi maksumust, s.o. kütteenergia kulud. U 2 garanteerib lineaarsetes regulaatorites teostamatute seaduste puudumise, see tagab juhtimistoimingute puudumise, mille korral kiirus muutub lõpmatuseks.
Juba olemasolu (3) tagab süsteemi stabiilsuse. Analüütilises disainis on ülesandeks leida analüütilisel kujul funktsioon Ф (U, U, x 1 ... xk) = 0 (5) - mis, võttes arvesse taimevõrrandeid ja piirtingimusi (1) ja (2) ), annaks integraalile minimaalse ( 3).
6.2.1. Probleemide sõnastamine ja klassifitseerimine optimaalse juhtimise teoorias. Valdav enamus meie käsitletud probleemidest jäeti sulgudest välja tegurid, mis on seotud uuritavate objektide ja süsteemide muutumisega aja jooksul. Võib-olla, kui teatud eeldused on täidetud, on selline lähenemine konstruktiivne ja õigustatud. Samas on ka selge, et see ei ole alati vastuvõetav. On ulatuslik ülesannete klass, mille puhul on vaja leida objekti optimaalsed tegevused, võttes arvesse selle olekute dünaamikat ajas ja ruumis. Nende lahendamise meetodid on optimaalse kontrolli matemaatilise teooria teema.
Väga üldisel kujul võib optimaalse kontrolliprobleemi sõnastada järgmiselt:
On mingi objekt, mille olekut iseloomustavad kahte tüüpi parameetrid - olekuparameetrid ja juhtimisparameetrid ning olenevalt viimase valikust kulgeb objekti haldamise protsess ühel või teisel viisil. Juhtimisprotsessi kvaliteeti hinnatakse mõne funktsiooni* abil, mille alusel püstitatakse ülesanne: leida selline juhtimisparameetrite väärtuste jada, mille puhul see funktsioon omandab äärmusliku väärtuse.
* funktsionaalsust Kutsutakse numbrilist funktsiooni, mille argumendid on reeglina teised funktsioonid.
Formaalsest vaatenurgast saab paljud optimaalse juhtimise probleemid taandada suurte mõõtmetega lineaarse või mittelineaarse programmeerimise probleemideks, kuna olekuruumi iga punkt vastab oma tundmatute muutujate vektorile. Sellegipoolest ei too selles suunas liikumine ilma vastavate ülesannete eripära arvestamata reeglina kaasa ratsionaalseid ja tõhusaid algoritme nende lahendamiseks. Seetõttu seostatakse optimaalsete juhtimisprobleemide lahendamise meetodeid traditsiooniliselt teise matemaatilise aparaadiga, mis pärineb variatsioonide arvutamisest ja integraalvõrrandite teooriast. Samuti tuleb märkida, et taas ajaloolistel põhjustel oli optimaalse juhtimise teooria keskendunud füüsilistele ja tehnilistele rakendustele ning selle rakendamine majandusprobleemide lahendamisel on teatud mõttes teisejärguline. Samal ajal võivad optimaalse kontrolli teooria aparaati kasutavad uurimismudelid mitmel juhul anda sisukaid ja huvitavaid tulemusi.
Eespool öeldule on vaja lisada märkus optimaalse juhtimisprobleemide lahendamiseks kasutatavate meetodite ja dünaamilise programmeerimise vahel valitseva tiheda seose kohta. Mõnel juhul saab neid kasutada alternatiivsel alusel, teistel aga täiendavad nad üksteist üsna edukalt.
Optimaalsete kontrolliprobleemide klassifitseerimiseks on erinevaid lähenemisviise. Esiteks saab neid liigitada sõltuvalt juhtimisobjektist:
Ø Ø juhtimisülesanded koos koondatud parameetrid;
Ø Ø objektihaldusülesanded koos jaotatud valikud.
Esimese näiteks on lennuki kui terviku juhtimine ja teisena pideva tehnoloogilise protsessi juhtimine.
Olenevalt tulemuste tüübist, milleni rakendatud kontrollid viivad, on neid deterministlik ja stohhastilineülesandeid. Viimasel juhul on kontrolltulemuseks tulemuste kogum, mida kirjeldatakse nende esinemise tõenäosustega.
Vastavalt kontrollitava süsteemi muutumise olemusele aja jooksul eristatakse ülesandeid:
Ø Ø diskreetse muutuv aeg;
Ø Ø s pidevalt muutuv aeg.
Diskreetse või pideva võimalike olekute hulgaga objektide haldamise probleemid liigitatakse sarnaselt. Juhtimisülesandeid süsteemide jaoks, milles aeg ja olekud muutuvad diskreetselt, nimetatakse juhtimisülesanneteks. riigimasinad. Lõpuks võib teatud tingimustel tekkida probleeme segasüsteemide juhtimisega.
Paljud juhitavate süsteemide mudelid põhinevad diferentsiaalvõrrandite aparaadil nii tavalistes kui ka osatuletistes. Jaotatud parameetritega süsteemide uurimisel eristatakse sõltuvalt kasutatavate osadiferentsiaalvõrrandite tüübist selliseid optimaalseid juhtimisprobleeme nagu paraboolne, elliptiline või hüperboolne.
Vaatleme kahte lihtsaimat näidet majandusobjektide haldamise probleemidest.
Probleem ressursside jaotamisel. Saadaval T numbritega laod i (i∊1:m), mis on ette nähtud homogeense toote säilitamiseks. Diskreetsetel aegadel t∊0:(T-l) jaotatakse numbritega tarbimisobjektide (klientide) vahel j, j∊1:n. Laovarude täiendamine toodete ladustamispunktides aastal t-nda ajahetke määrab kogused a i t,i∊1:m, ja klientide vajadused selles on võrdsed b j t, j∊1:n. Tähistage c t i,j on toote ühiku tarnimise maksumus i ladu j-th tarbija hetkel t. Samuti eeldatakse, et toode, mis saabus lattu omal ajal t, saab kasutada alates järgmisest hetkest ( t+l). Koostatud mudeli jaoks on ülesandeks leida selline ressursside jaotusplaan ( x t i,j} Tm x n, mis minimeerib kogu süsteemi kogu tööperioodi jooksul ladudest tarbijatele toodete tarnimise kulu.
Märgistades läbi x t i,j tarnitud toote kogus j-th klient koos i ladu sisse t-th ajahetkel ja pärast seda z t i- toote koguhulk i ladu, võib ülalkirjeldatud probleemi kujutada selliste muutujate kogumite leidmise probleemina
mis vähendavad funktsiooni

tingimustel

kus toote esialgsete laovarude mahud ladudes z 0 i = ž i. eeldatakse, et need on antud.
Ülesanne (6.20)-(6.23) kutsutakse üles lineaarse programmeerimise dünaamilise transpordi probleem. Ülaltoodud terminoloogia poolest sõltumatud muutujad x t i,j esindama juhtimisparameetrid süsteem ja neist sõltuvad muutujad z t i- täitematerjal oleku parameetrid süsteemid igal ajahetkel. t. Piirangud z t i≥ 0 garantii, et igal ajal ei saa ühestki laost eksportida oma tegelikku kogust ületavat tootemahtu ning piirangud (6.21) seavad reeglid selle koguse muutmiseks ühest perioodist teise liikumisel. Tavaliselt kutsutakse seda tüüpi piiranguid, mis seavad tingimused süsteemi olekuparameetrite väärtustele faasis.
Samuti märgime, et tingimus (6.21) on faasipiirangute lihtsaim näide, kuna kahe kõrvutise perioodi olekuparameetrite väärtused on seotud t ja t+l. Üldjuhul saab sõltuvuse tuvastada parameetrite rühmale, mis kuulub mitmesse, võib-olla mitte külgnevasse etappi. Selline vajadus võib tekkida näiteks mudelite tarnete hilinemise teguri arvessevõtmisel.
Makromajanduse lihtsaim dünaamiline mudel. Esitagem teatud piirkonna majandust kogumina P tööstused ( j∊1:P), mille koguprodukt mingil hetkel rahas väljendatuna t saab esitada vektorina z t=(z t 1 , z t 2 ,..., z t n), kus t∊0:(T-üks). Tähistage A t otsekulude maatriks, mille elemendid a t i,j, kajastavad tootmiskulusid i-th tööstusharu (rahalises väärtuses) toodanguühiku valmistamiseks j tööstusharu sisse t- ajahetk. Kui X t= ║x t i,j║n x m- maatriks, mis määrab konkreetsed tootmisnormid i tööstusharu kavatseb tootmist laiendada j tööstusharu ja kell t = (kell t 1 , kell t 2 , ..., aadressil tn) on tarbimiseks kasutatavate tarbimissektorite tootmismahtude vektor, siis võib laiendatud taastootmise tingimuse kirjutada järgmiselt.
kus z 0 = ž - eeldatakse, et tööstusharude toodete esialgne tarne on antud ja
Vaadeldavas mudelis kogused z t on süsteemi oleku parameetrid ja X t- juhtimisparameetrid. Selle alusel saab püstitada erinevaid ülesandeid, mille tüüpiliseks esindajaks on hetkel majanduse optimaalse väljundi probleem T mõnele antud riigile z*. See probleem taandub juhtimisparameetrite jada leidmisele

tingimuste (6.24)-(6.25) täitmine ja funktsiooni minimeerimine
6.2.2. Lihtsaim optimaalse kontrolli probleem.Üks äärmuslike probleemide lahendamise tehnikaid on isoleerida mõni probleem, mis lubab suhteliselt lihtsat lahendust, millele saab tulevikus taandada muid probleeme.
Mõelge nn lihtsaim kontrolliprobleem. Ta näeb välja nagu

Ülesande (6.27)-(6.29) tingimuste spetsiifilisus seisneb selles, et juhtimiskvaliteedi funktsioonid (6.27) ja piirangud (6.28) on lineaarsed. z t, samal ajal funktsiooni g(t, x t) in (6.28) võib olla suvaline. Viimane omadus muudab probleemi isegi jaoks mittelineaarseks t=1, st staatilises versioonis.
Ülesande (6.27)-(6.29) lahendamise üldine idee taandatakse selle "jagamisele" alamülesanneteks iga üksiku ajahetke jaoks, eeldusel, et need on edukalt lahendatavad. Ehitame ülesande (6.27)-(6.29) jaoks Lagrange'i funktsiooni

kus λ t- Lagrange'i kordajate vektor ( t∊0:T). Piirangud (6.29), mis on üldist laadi, ei sisaldu antud juhul funktsioonis (6.30). Kirjutame selle veidi teistsugusel kujul

Funktsiooni Ф ekstreemumi vajalikud tingimused (x, z,λ) vektorite hulga järgi z t on antud võrrandisüsteemiga
mida nimetatakse konjugeeritud muutujate süsteem. Nagu näete, parameetrite λ leidmise protsess t süsteemis (6.32) teostatakse korduvalt vastupidises järjekorras.
Lagrange'i funktsiooni ekstreemumi vajalikud tingimused muutujates λ t on samaväärne piirangutega (6.28) ja lõpuks selle ekstreemumi tingimustega vektorite hulga suhtes x t∊X t, t∊1:(T-1) tuleb ülesande lahendamise tulemusena leida
Seega taandub optimaalse kontrolli leidmise probleem optimaalsuse kahtlusega juhtelementide leidmisele, st sellistele, mille jaoks vajalik optimaalsuse tingimus on täidetud. See omakorda taandub selliste leidmisele t, t, t, rahuldades tingimuste süsteemi (6.28), (6.32), (6.33), mis on nn. diskreetne Pontrjagini maksimumpõhimõte.
Teoreem on õige.
Tõestus.
Lase t, t, t, rahuldada süsteem (6.28), (6.32), (6.33). Siis tuleneb (6.31) ja (6.32), et

ja sellest ajast peale t rahuldab (6,33), siis
Teisest küljest tuleneb (6.28)-st (6.30), et iga vektori korral t
Seega
Rakendades teoreemi (6.2), aga ka mittelineaarse programmeerimise teooria sätteid ekstreemülesande lahenduse ja sadulapunkti olemasolu vahelise seose kohta (vt ptk 2.2.2), järeldame, et vektorid t, t on lahendus lihtsaimale optimaalsele juhtimisülesandele (6.27)-(6.29).
Selle tulemusena saime selle ülesande lahendamiseks loogiliselt lihtsa skeemi: seosed (6.32) määravad konjugeeritud muutujad t, siis ülesande (6.33) lahendamise käigus leitakse juhtelemendid t ja kaugemal (6.28) - olekute optimaalne trajektoor t,.
Kavandatud meetod kuulub optimaalse juhtimise teooria põhitulemuste hulka ja, nagu eespool mainitud, on oluline paljude keerukamate probleemide lahendamiseks, mis ühel või teisel viisil on taandatud kõige lihtsamatele. Samas on ilmselged ka selle efektiivse kasutamise piirid, mis sõltuvad täielikult probleemi (6.33) lahendamise võimalusest.
PÕHIMÕISTED
Ø Ø Mäng, mängija, strateegia.
Ø Ø Nullsummamängud.
Ø Ø Matrix mängud.
Ø Ø Antagonistlikud mängud.
Ø Ø Maksimi ja miinimumi põhimõtted.
Ø Ø Mängu sadulapunkt.
Ø Ø Mängu hind.
Ø Ø Segastrateegia.
Ø Ø Maatriksmängude põhiteoreem.
Ø Ø Dünaamiline transpordi probleem.
Ø Ø Makromajanduse lihtsaim dünaamiline mudel.
Ø Ø Lihtsaim optimaalse juhtimise probleem.
Ø Ø Diskreetne Pontrjagini maksimumprintsiip.
KONTROLLKÜSIMUSED
6.1. Sõnastage lühidalt mänguteooria kui teadusdistsipliini teema.
6.2. Mida tähendab sõna "mäng"?
6.3. Kirjeldamaks, millistes majandusolukordades saab mänguteooria aparaati rakendada?
6.4. Mis on antagonistlik mäng?
6.5. Mis määrab unikaalselt maatriksmängud?
6.6. Millised on maximini ja minimaxi põhimõtted?
6.7. Millistel tingimustel saame öelda, et mängul on sadulapunkt?
6.8. Too näiteid mängudest, millel on sadulapunkt ja millel pole.
6.9. Millised lähenemisviisid on olemas optimaalsete strateegiate määramiseks?
6.10. Mida nimetatakse "mängu hinnaks"?
6.11. Defineerige mõiste "segastrateegia".
BIBLIOGRAAFIA
1. Abramov L. M., Kapustin V. F. Matemaatiline programmeerimine. L., 1981.
2. Ašmanov S. A. Lineaarne programmeerimine: Proc. toetust. M., 1981.
3. Ašmanov S. A., Tihhonov A. V. Optimeerimise teooria ülesannetes ja harjutustes. M., 1991.
4. Bellman R. Dünaamiline programmeerimine. M., 1960.
5. Bellman R., Dreyfuss S. Dünaamilise programmeerimise rakendusprobleemid. M., 1965.
6. Gavurin M. K., Malozemov V. N.Äärmuslikud probleemid lineaarsete piirangutega. L., 1984.
7. Gaas S. Lineaarne programmeerimine (meetodid ja rakendused). M., 1961.
8. Gale D. Lineaarsete majandusmudelite teooria M., 1963.
9. Gill F., Murray W., Wright M. Praktiline optimeerimine / Per. inglise keelest. M., 1985.
10. Davõdov E. G. Operatsiooniuuringud: Proc. toetus ülikooli üliõpilastele. M., 1990.
11. Danzig J. Lineaarne programmeerimine, selle üldistused ja rakendused. M., 1966.
12. Eremin I. I., Astafjev N. N. Sissejuhatus lineaarse ja kumera programmeerimise teooriasse. M., 1976.
13. Ermoliev Yu.M., Ljaško I.I., Mihhalevitš V.S., Tyuptya V.I. Operatsioonide uurimise matemaatilised meetodid: Proc. toetus ülikoolidele. Kiiev, 1979.
14. Zaichenko Y.P. Operatsiooniuuringud, 2. väljaanne. Kiiev, 1979.
15. Zangwill W.I. Mittelineaarne programmeerimine. Ühtne lähenemine. M., 1973.
16. Zeutendijk G. Võimalike suundade meetodid. M., 1963.
17. Karlin S. Matemaatilised meetodid mänguteoorias, programmeerimises ja majanduses. M., 1964.
18. Karmanov V.G. Matemaatiline programmeerimine: Proc. toetust. M., 1986.
19. Korbut A.A., Finkelyitein Yu. Yu. Diskreetne programmeerimine. M., 1968.
20. Kofman A., Henri-Laborder A. Operatsioonide uurimise meetodid ja mudelid. M., 1977.
21. Künze G.P., Crelle V. Mittelineaarne programmeerimine. M., 1965.
22. Ljašenko I.N., Karagodova E.A., Tšernikova N.V., Shor N.3. Lineaarne ja mittelineaarne programmeerimine. Kiiev, 1975.
23. McKinsey J. Sissejuhatus mänguteooriasse. M., 1960.
24. Mukhacheva E. A., Rubinstein G. Sh. Matemaatiline programmeerimine. Novosibirsk, 1977.
25. Neumann J., Morgenstern O. Mänguteooria ja majanduslik käitumine. M, 1970.
26. Maagi O. Graafiteooria. M., 1968.
27. Taha X. Sissejuhatus operatsiooniuuringutesse / Per. inglise keelest. M., 1985.
28. Fiakko A., McCormick G. Mittelineaarne programmeerimine. Järjestikuse tingimusteta minimeerimise meetodid. M., 1972.
29. Hadley J. Mittelineaarne ja dünaamiline programmeerimine. M., 1967.
30. Yudin D.B., Holstein E.G. Lineaarne programmeerimine (teooria, meetodid ja rakendused). M., 1969.
31. Yudin D.B., Holstein E.G. Lineaarne programmeerimine. Teooria ja lõplikud meetodid. M., 1963.
32. Lapin L. Kvantitatiivsed meetodid juhtumitega äriotsuste tegemiseks. Neljas väljaanne. HBJ, 1988.
33. Liitle I.D.C., Murty K.G, Sweeney D.W., Karel C. Algoritm reisimiseks reisiva müügimehe probleemi lahendamiseks. - Operatsiooniuuringud, 1963, kd 11, nr. 6, lk. 972-989/ Vene. trans.: Little J., Murthy K., Sweeney D., Kerel K. Algoritm rändmüüja probleemi lahendamiseks. - Raamatus: Economics and Mathematical Methods, 1965, kd 1, nr 1, lk. 94-107.
EESSÕNA .................................................. .............................................................. ............................................................ ...................................................... ...................... 2
SISSEJUHATUS .................................................. ................................................... ................................................... . ................................................ .. ........ 3
PEATÜKK 1. LINEAARNE PROGRAMMEERIMINE ................................................ .................................................. ................................................................ ......... kaheksa
1.1. LINEAARSE PROGRAMMEERIMISE PROBLEEMI SÕNASTAMINE ................................................... ................................................................ ................ 9
1.2. ZLP PEAMISED OMADUSED JA SELLE ESIMESE GEOMEETRILINE TÕLGENDUS................................................ ................................................................ üksteist
1.3. PÕHILAHENDUSED JA ZLP TEINE GEOMEETRILINE TÕLGENDUS................................................ ................................................................ ...... 15
1.4. LIHTNE MEETOD................................................ ................................................... . ................................................ .. ...................................... 17
1.5. MUUDATUD LIHTNE MEETOD................................................... ................................................................ ................................................................ ......... 26
1.6. DUAALSUSE TEOORIA LINEAARSES PROGRAMMEERIMISES................................................ ................................................................ .............................. kolmkümmend
1.7. KAHELINE LIHTNE MEETOD................................................ ................................................................ ................................................................ .................. .37
PÕHIMÕISTED................................................ ............................................................ .............................................................. .............................................................. 42
KONTROLLKÜSIMUSED................................................ ................................................... . ................................................ .. .............................. 43
PEATÜKK 2. MITTELINEAARNE PROGRAMMEERIMINE ................................................ .............................................................. .............................................................. ... 44
2.1. MEETODID MITTELINEAARSE PROGRAMMEERIMISPROBLEEMIDE LAHENDAMISEKS................................................ ................................................................ .............................. 44
2.2. DUAALSUS MITTELINEAARSES PROGRAMMEERIMISES................................................ ................................................................ ................................... ... 55
PÕHIMÕISTED................................................ ............................................................ .............................................................. .............................................................. ............ 59
KONTROLLKÜSIMUSED................................................ ................................................... ................................................ .. .............................. 59
PEATÜKK 3. TRANSPORT- JA VÕRGUÜLESANDED ............................................ ................................................................ ................................................................ ... 60
3.1. TRANSPORTPROBLEEM JA SELLE LAHENDUSMEETODID ................................................ ................................................................ .............................................. 60
3.2. VÕRGUÜLESANDED................................................ ................................................................ .................................................. ................................................................ .............. 66
PÕHIMÕISTED................................................ ............................................................ .............................................................. .............................................................. 73
KONTROLLKÜSIMUSED................................................ ................................................... . ................................................ .. .............................. 73
4. PEATÜKK. DISKREETNE PROGRAMMEERIMINE ................................................. .................................................. ................................................................ .. 74
4.1. DISKREETSETE PROGRAMMEERIMISÜLESANDE LIIGID................................................ ................................................................ ................................................................ ..... 74
4.2. GOMORY MEETOD................................................................ .................................................. ................................................... ................................................ 78
4.3. HARU- JA SÖÖTAMISMEETOD................................................ ...................................................... ...................................................... .......................................... 81
PÕHIMÕISTED................................................ ............................................................ .............................................................. .............................................................. 86
KONTROLLKÜSIMUSED................................................ ................................................... . ................................................ .. .............................. 86
PEATÜKK 5. DÜNAAMILINE PROGRAMMEERIMINE ................................................... .................................................. .............................................. 86
5.1. DÜNAAMILISTE PROGRAMMEERIMISMEETODITE ÜLDSKEEM................................................ ................................................................ ........................ 86
5.2. DÜNAAMILISTE PROGRAMMEERIMISÜLESANDE NÄITED................................................ ................................................................ ................................................ 93
PÕHIMÕISTED................................................ ............................................................ .............................................................. .............................................. 101
KONTROLLKÜSIMUSED................................................ ................................................... ................................................ .. ................................ 101
PEATÜKK 6. ÜLEVAADE TEGEVUSE UURINGU TEISTEST JAOTSETEST................................................. .............................................. 101
6.1. MÄNGUTEOORIA................................................ ................................................... ................................................ .. ................................................ 101
6.2. OPTIMAALSE JUHTIMISE TEOORIA................................................ ................................................................ ................................................................ .......................... 108
PÕHIMÕISTED................................................ ............................................................ .............................................................. .............................................. 112
KONTROLLKÜSIMUSED................................................ ................................................... ................................................ .. ...................... 112
BIBLIOGRAAFIA................................................ . ................................................ .. ................................................................ ................................ 112
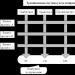
Igasugune automaatsüsteem on mõeldud mingi objekti juhtimiseks, see peab olema ehitatud nii, et selle juhtimine oleks optimaalne ehk ühes või teises mõttes parim. Optimaalse juhtimise probleemid tekivad kõige sagedamini protsessijuhtimise alamsüsteemides. Igal juhul on teatud tehnoloogiline ülesanne, mille jaoks on ette nähtud vastav masin või paigaldis (juhtimisobjekt), mis on varustatud vastava juhtimissüsteemiga, s.o. me räägime mõnest ACS-ist, mis koosneb juhtimisobjektist ja seadmete komplektist, mis võimaldavad seda objekti juhtida. Reeglina sisaldab see komplekt mõõte-, võimendus- ja muundusseadmeid. Kui ühendate võimendus-, teisendus- ja käitamisseadmed üheks lüliks, mida nimetatakse juhtseadmeks või regulaatoriks, saab ACS-i funktsionaalse diagrammi viia joonisel fig. üksteist.
Riis. 12 Optimaalse süsteemi funktsionaalne diagramm
Juhtseadme sisend saab seadistustoimingu, mis sisaldab juhiseid selle kohta, milline peaks olema objekti olek - nn "soovitav olek".
Juhtobjekt võib saada häiriva tegevuse z, mis tähistab koormust või häireid. Mõõteseadmega objekti koordinaatide mõõtmist saab teostada mõne juhusliku veaga x (error) .
Seega on juhtseadme ülesandeks sellise juhtimistoimingu väljatöötamine, et ACS-i kui terviku funktsioneerimise kvaliteet oleks teatud mõttes parim. Juhtseadme algoritmi määramiseks on vaja teada objekti omadusi ning juhtseadmesse siseneva objekti ja häirete kohta info olemust.
Objekti omaduste all mõistame objekti väljundväärtuste sõltuvust sisendist
kus F on üldiselt operaator, mis kehtestab vastavusseaduse kahe funktsioonikomplekti vahel. Objekti operaatorit F saab määrata mitmel viisil: kasutades valemeid, tabeleid, graafikuid. See on seatud ka diferentsiaalvõrrandisüsteemi kujul, mis vektori kujul on kirjutatud kui
kus ja neile anti vektori alg- ja lõppväärtused.
Vaadeldava probleemi lahendamiseks on palju erinevaid viise. Kuid ainult üks viis objekti haldamiseks annab mõnes mõttes parima tulemuse. Seda juhtimismeetodit ja seda rakendavat süsteemi nimetatakse optimaalseks.
Et oleks kvantitatiivne alus ühe kontrollimeetodi eelistamiseks teistele, on vaja määrata kontrollieesmärk ning seejärel võtta kasutusele eesmärgi saavutamise tulemuslikkust iseloomustav meede - kontrolli optimaalsuse kriteerium. Tavaliselt on optimaalsuse kriteeriumiks arvuline väärtus, mis sõltub süsteemi ajas ja ruumis muutuvatest koordinaatidest ja parameetritest, nii et igale juhtimisseadusele vastab teatud kriteeriumi väärtus. Optimaalsuse kriteeriumiks saab valida erinevaid vaadeldava protsessi tehnilisi ja majanduslikke näitajaid.
Mõnikord esitatakse juhtimissüsteemile erinevad, mõnikord vastuolulised nõuded. Puuduvad kontrolliseadused, mis vastaksid igale nõudele samal ajal parimal viisil. Seetõttu peate kõigi nõuete hulgast valima ühe peamise, mis peaks olema parimal viisil täidetud. Muud nõuded mängivad piirangute rolli. Seetõttu tuleks optimaalsuse kriteeriumi valikul lähtuda vaid vaadeldava objekti ja keskkonna tehnoloogia ja ökonoomika uurimisest. See ülesanne ületab operatsioonivõimendite teooriat.
Optimaalse kontrolli ülesannete lahendamisel on kõige olulisem seada kontrolli eesmärk, mida matemaatiliselt võib pidada teatud väärtuse Q - optimaalsuse kriteeriumi - ekstreemumi saavutamise probleemiks. Matemaatikas nimetatakse sellist suurust funktsionaalseks. Sõltuvalt lahendatavast probleemist on vaja saavutada minimaalne või maksimaalne Q. Näiteks kirjutame optimaalsuse kriteeriumi, milles Q peaks olema minimaalne
Nagu näha, sõltub Q väärtus funktsioonidest.
Optimaalsuse kriteeriumina võib võtta erinevaid tehnilisi ja tehnilis-majanduslikke näitajaid ja hinnanguid. Optimaalsuse kriteeriumi valik on insenertehniline ja insener-majanduslik ülesanne, mis lahendatakse juhitava protsessi põhjaliku ja tervikliku uurimise alusel. Juhtimise teoorias kasutatakse laialdaselt integraalfunktsionaale, mis iseloomustavad süsteemi toimimise kvaliteeti. Selle funktsiooni maksimaalse või minimaalse väärtuse saavutamine näitab süsteemi optimaalset käitumist või olekut. Integraalsed funktsioonid peegeldavad tavaliselt juhtimisobjektide töötingimusi ja võtavad arvesse koordinaatidele seatud piiranguid (küte, tugevus, energiaallikate võimsus jne).
Juhtimisprotsesside jaoks kasutatakse järgmisi kriteeriume:
1. optimaalne jõudlus (üleminekuaeg)
2. minimaalne ruutkeskmine viga.
3. minimaalne energiatarbimine.
Seega võib optimaalsuse kriteerium viidata ülemineku- või püsivale protsessile süsteemis.
Sõltuvalt optimaalsuse kriteeriumist saab optimaalsed süsteemid jagada kahte põhiklassi – optimaalne kiiruselt ja optimaalne täpsus.
Optimaalsed juhtimissüsteemid võib sõltuvalt optimaalsuse kriteeriumi olemusest jagada kolme tüüpi:
a) ühtlaselt optimaalsed süsteemid;
b) statistiliselt optimaalsed süsteemid;
c) minimax-optimaalsed süsteemid.
Ühtlaselt optimaalne on süsteem, milles iga üksik protsess on optimaalne. Näiteks kiirusoptimaalsetes süsteemides jõuab süsteem mis tahes algtingimuste ja häirete korral nõutavasse olekusse lühima aja jooksul.
Statistiliselt optimaalsetes süsteemides on optimaalsuse kriteerium statistiline. Sellised süsteemid peaksid olema keskmiselt parimad. Siin ei ole iga eraldi protsessi optimeerimine vajalik või võimatu. Statistilise kriteeriumina esineb kõige sagedamini esmase kriteeriumi keskmine väärtus, näiteks matemaatiline ootus teatud väärtusele, mis läheb üle teatud piiride.
Minimax-optimaalsed süsteemid on süsteemid, mis halvimal juhul annavad parima võimaliku tulemuse. Need erinevad ühtlaselt optimaalsetest selle poolest, et mitte halvimal juhul võivad need anda kehvema tulemuse kui ükski teine süsteem.
Sõltuvalt hallatava objekti kohta teabe hankimise meetodist võib optimaalsed süsteemid jagada ka kolme tüüpi:
optimaalsed süsteemid täieliku teabega objekti kohta;
optimaalsed süsteemid mittetäieliku teabega objekti ja selle passiivse akumulatsiooni kohta;
optimaalsed süsteemid, millel on puudulik teave objekti kohta ja selle aktiivne kogunemine juhtimisprotsessis (kahejuhtimissüsteemid).
Süsteemi optimaalse sünteesi probleeme on kahte tüüpi:
Kontrolleri parameetrite optimaalsete väärtuste määramine objekti antud parameetrite ja süsteemi antud struktuuri jaoks;
Kontrolleri struktuuri süntees ja parameetrite määramine etteantud parameetrite ja juhtimisobjekti struktuuri jaoks.
Esimest tüüpi ülesannete lahendamine on võimalik erinevate analüütiliste meetoditega integraalhinnanguid minimeerides, samuti arvutitehnoloogia (arvutimodelleerimine) abil, arvestades etteantud optimaalsuse kriteeriumi.
Teist tüüpi ülesannete lahendamine põhineb erimeetodite kasutamisel: klassikalise variatsiooniarvutuse meetodid, Pontrjagini maksimumprintsiip ja Bellmani dünaamiline programmeerimine, samuti matemaatilise programmeerimise meetodid. Optimaalsete süsteemide sünteesimiseks juhuslike signaalidega kasutatakse Wieneri meetodeid, variatsiooni- ja sagedusmeetodeid. Adaptiivsete süsteemide väljatöötamisel kasutatakse enim gradientmeetodeid, mis võimaldavad määrata seaduspärasusi, reguleeritavate parameetrite muutusi.
Viimastel aastatel on optimaalset juhtimist kasutatud nii tehnilistes süsteemides tootmisprotsesside efektiivsuse tõstmiseks kui ka organisatsiooni juhtimissüsteemides ettevõtete, organisatsioonide ja rahvamajanduse sektorite tegevuse parandamiseks.
Organisatsioonisüsteemides on tavaline, et huvi tunneb meeskonna lõppmängu tulemus ilma uurimata
kasutegur käskluse andmise ja lõpptulemuse saamise vahelises siirdeprotsessis. See on seletatav asjaoluga, et tavaliselt sellistes süsteemides on siirdeprotsessi kaod üsna väikesed ega mõjuta oluliselt koguvõimendust püsiseisundis, kuna püsiseisund ise on palju pikem kui mööduv protsess. Kuid mõnikord ei uurita dünaamikat matemaatiliste raskuste tõttu. Meetodite kursused on pühendatud organisatsiooni- ja majandussüsteemide lõppseisundite optimeerimise meetoditele. optimeerimise ja operatsioonide uuringud.
Dünaamiliste tehniliste süsteemide juhtimisel on optimeerimine sageli hädavajalik just siirdeprotsesside puhul, mille puhul efektiivsusnäitaja ei sõltu mitte ainult koordinaatide hetkeväärtustest (nagu äärmuslikul juhtimisel), vaid ka muutuse olemusest. minevik, olevik ja tulevik ning seda väljendavad mõned funktsioonid koordinaatidel, nende tuletistel ja võib-olla ka ajas.
Näitena võib tuua sportlase distantsijooksu juhtimise. Kuna tema energiavaru piiravad füsioloogilised tegurid ning reservi kulu sõltub jooksu iseloomust, ei saa sportlane enam igal hetkel maksimaalset võimalikku jõudu anda, et mitte enneaegselt energiavaru ära kasutada ja jooksma jätta. distantsilt väljas, kuid peab otsima oma omadustele vastavat optimaalset jooksurežiimi.
Optimaalse juhtimise leidmine sellistes dünaamilistes ülesannetes nõuab juhtimisprotsessis üsna keeruka matemaatilise probleemi lahendamist variatsioonide arvutamise või matemaatilise programmeerimise meetodite abil, olenevalt süsteemi matemaatilise kirjelduse (matemaatilise mudeli) tüübist. Seega saab arvutusseade või arvuti optimaalse juhtimissüsteemi orgaaniliseks komponendiks. Põhimõte on illustreeritud joonisel fig. 1.10. VM-i arvutusseadme (masina) sisend saab teavet koordinaatide x hetkeväärtuste kohta objekti O väljundist, juhtelementide ja selle sisendist, välismõjude z kohta objektile, samuti erinevate tingimuste seadmine väljastpoolt: piirtingimuste optimaalsuskriteeriumi väärtus teave lubatud väärtuste kohta Arvutuslik
Riiklik õppeasutus
erialane kõrgharidus
Moskva Füüsika ja Tehnoloogia Instituut
(Riigiülikool)
KINNITA
Õppeprorektor
Yu.A.Samarsky
"________" _______________ 2004
PROGRAMM
kursusel: OPTIMAALNE KONTROLL
suunas 511600
FUPM-i teaduskond
Kontrolli matemaatiliste aluste osakond
hästi IV
semester 7, 8
loengud - 50 tundi. Eksam - 8 semester
seminarid - 50 tundi. Ainepunkt - 7. semester
laborid - ei
Iseseisev töö - 2 tundi nädalas
TUNDI KOKKU 100
Programmi ja ülesande koostasid: füüsika- ja matemaatikateaduste doktor, professor Zhadan V.G.
Osakonnajuhataja S.A. Hani
1. Optimaalse kontrolli põhiprobleem. L.S. maksimumpõhimõte Pontrjagin (miinimumpõhimõte). Kanooniline märge. Maksimaalne põhimõte juhtimisparameetreid sisaldavate süsteemide jaoks.
2. Probleemid liikuva parempoolse otsaga. transversaalsuse tingimused. Lagrange'i ja Bolzi probleemid. Mayeri ja Lagrange'i probleemid fikseerimata protsessi lõpetamise ajaga. Kiirusülesanne. Probleem liikuva vasaku otsaga.
3. Maksimumprintsiibi tõendamine L.S. Pontrjagin Mayeri probleemi eest. Nõela variatsiooni mõiste. Gronwall-Bellmani lemma. Optimeerimise arvestamine juhtimisparameetrite järgi.
4. Maksimumprintsiibi seos variatsiooniarvutusega. Euleri võrrand. Euleri võrrandi esimesed integraalid. Weerstrassi, Legendre ja Jacobi tingimused. Jacobi võrrand. Weerstrass–Erdmanni tingimused.
5. Lineaarsed süsteemid. Lineaarsete süsteemide maksimaalne põhimõte. Lõpliku arvu lülituspunktide teoreem.
6. Kättesaadavuse komplekt lineaarsetele süsteemidele. Äärmuslik kontroll ja äärmuslik põhimõte.
7. Punktide juhitavus lineaarsete süsteemide jaoks. Punkti juhitavuse kriteerium. Kalmani teoreem punktide juhitavuse kohta. Lineaarsete süsteemide täielik juhitavus. Kalmani teoreem autonoomsete süsteemide täieliku juhitavuse kohta.
8. Vaadeldavuse probleem. Lineaarsüsteemi vaadeldavuse kriteerium. Algseisundi jälgimine. Vaadeldavuse ja juhitavuse seos. Statsionaarse süsteemi täieliku vaadeldavuse kriteerium.
9. Lagrange'i formalism ja selle kasutamine optimaalsete juhtimisülesannete lahendamisel. Optimaalse kontrolli sünteesi probleem.
10. Identifitseerimise probleem. Identifitseerimiskriteerium. Statsionaarse süsteemi täieliku identifitseeritavuse kriteerium.
11. Katkestatavate parempoolsete külgedega süsteemid. Hüppe tingimus.
12. Invariantsete süsteemide mõiste. Dünaamiliste süsteemide omadused. Impulsside võrdlusväli. Invariantsuse vajalikud ja piisavad tingimused. korrigeeriv funktsioon.
13. Optimaalsuseks piisavad tingimused. Äärmuste valdkond. Seos piisavate Weerstrassi tingimustega variatsiooniarvutuse klassikalise probleemi jaoks.
14. Dünaamilise programmeerimise teooria elemendid. Optimaalsuseks vajalikud tingimused. Piisavad optimaalsuse tingimused. Bellmani võrrand. Dünaamilise programmeerimise maksimumprintsiibi tuletamine. Seos variatsiooniarvutusega.
15. Piirväärtusülesannete lahendamise meetodid. Newtoni meetodi rakendamine. Piirtingimuste ülekandmine. Pühkimismeetod mittelineaarsete probleemide jaoks.
16. Variantide järjestikusel analüüsil põhinevad numbrilised meetodid. Kiievi luudameetod, rändtoru meetod, kohalike variatsioonide meetod.
17. Numbrilised meetodid, mis põhinevad taandamisel mittelineaarsetele programmeerimisülesannetele. Juhtvektori komponentide suhtes tuletiste arvutamine diskreetsete protsesside korral. Karistusmeetod, laetud funktsionaalmeetod.
18. Diskreetse miinimumi põhimõte. Variatsioonilised ebavõrdsused. Tingimusliku gradiendi meetodi rakendamine optimaalsete juhtimisprobleemide lahendamiseks. Kvaasimiinimum põhimõte.
19. Piisava optimaalsuse tingimused V.F. Krotov pidevate ja diskreetsete protsesside jaoks. Taotlus V.F. Krotov lineaarülesannete lahendamiseks.
20. Spetsiaalsed juhtnupud. Spetsiaalsete juhtseadiste määratlus Poissoni sulgude abil. Kelly ja Kopp-Moyeri tingimused.
BIBLIOGRAAFIA
1. Moiseev N.N. Numbrilised meetodid optimaalsete süsteemide teoorias. – M.: Nauka, 1971.
2. Jevtušenko Yu.G. Ekstreemprobleemide lahendamise meetodid ja nende rakendamine optimeerimissüsteemides. – M.: Nauka, 1982.
3. Moisejev N.N., Ivanilov Yu.P., Stolyarova E.M. Optimeerimismeetodid. – M.: Nauka, 1987.
4. Pontrjagin L.S., Boltjanski V.G., Gamkrelidze Z.V., Mištšenko E.F. Optimaalsete protsesside matemaatiline teooria. – M.: Fizmatgiz, 1961.
5. Vassiljev F.P. Ekstreemsete probleemide lahendamise meetodid. – M.: Nauka, 1988.
6. Gabasov R., Kirillova F.M. Maksimaalne põhimõte optimaalse juhtimise teoorias. - Minsk: Teadus ja tehnoloogia, 1974.
7. Fleming W., Richel R. Deterministlike ja stohhastiliste süsteemide optimaalne juhtimine. – M.: Mir, 1978.
8. Optimaalse juhtimise teooria alused /Toim V.F. Krotov.- M .: Kõrgkool, 1990.
9. Lee E.B., Marcus P. Optimaalse juhtimise teooria alused. Moskva: Nauka, 1972.
10. Gabasov R., Kirillova F.M. Spetsiaalsed optimaalsed juhtnupud. – M.: Nauka, 1973.
Ülesannet saab vaadata