Optimális automata vezérlőrendszerek. Optimális automata vezérlőrendszerek osztályozása Angol tudósok munkarendszereinek optimális vezérlése

Az optimális ACS bizonyos értelemben a legjobb rendszer. Az optimalitási kritériumok eltérőek lehetnek, és függhetnek a megoldandó problémától. A leggyakoribb optimalitási kritériumok a következők:

1) Az ACS pontossága változó hatás mellett,

2) Átmeneti idő,

3) jövedelmezőség;

Teljesítmény;

Integrált kritériumok.

A mai napig a legnagyobb fejlesztés a rendszerek optimalitáselméletében 2 területet ért el:

1) A rendszerek mozgásának optimális szabályozásának elmélete teljes körű információval az objektumról és a zavarokról;

Az optimális szabályozás elméletei véletlenszerű perturbációk mellett.

Az optimális szabályozás megvalósításához szükséges:

Határozza meg az irányítás célját. A célt vagy egy célfüggvény vagy egy optimalizálási kritérium fejezi ki.

A célfüggvény vagy optimalizálási kritérium lehetővé teszi bármely megoldás mennyiségi hatásának megtalálását.

Válasszon modellt a döntés hatékonyságának elemzéséhez és meghatározásához.

Tanulmányozni az objektum működésének környezetének összes állapotát, amelyek befolyásolják a menedzsment folyamat múltját, jelenét és jövőjét.

Az optimális szabályozás problémájának megoldása során a variációs számítás módszereit, a maximum elveket, valamint a dinamikus és matematikai programozást alkalmazzák.

Az optimális szabályozási probléma általános esetben a következőképpen fogalmazható meg:

1) A menedzsment célja, matematikailag reprezentálva valamilyen funkcionális vagy irányítási kritérium formájában

2) Rendszeregyenletek - általában állapotegyenletek formájában adják meg

3) A határegyenletrendszer a kezdeti és a végső időpontban.

4) Kényszerrendszer, amelynek ki kell elégítenie az állapotváltozókat és egyenleteket.

Megkereséséhez szükséges:

Az a vezérlővektor, amelynél a kontrollcél kritériumának szélsősége van (max vagy min).

Megjegyzendő, hogy bizonyos esetekben nem létezik az optimális szabályozás, és ez a probléma megoldása nélkül nem ítélhető meg. Az optimális szabályozás megtalálásának problémájára a megoldás nem egyértelmű, i.e. minden talált megoldás helyi optimumot ad. Ha minden lokális optimum megtalálható, akkor ebben az esetben egy globális optimum azonosítható. A megtalált globális optimum az optimális szabályozási probléma megoldása.

Integrált minőségi kritériumok:

Optimális teljesítmény

A funkcionálisnak megvan a formája

Optimális teljesítmény

Az optimalitás kritériuma a  elfordulási szög egy bizonyos t ideig, és a funkcionális alakja

Optimális gazdaságosság

Az optimálisság kritériuma az energiafogyasztás egy bizonyos ideig, és a funkciónak megvan a formája

28. Szabályozók analitikai tervezése. A probléma megfogalmazása.

A lineáris automata vezérlőrendszerek tranziensek minőségének vizsgálata során kiömlött integrál minőségi kritériumokat vezettek be, amelyek segítségével a tranziens folyamatot végtelen időintervallumon keresztül értékelték. Az integrált minőségi kritériumok mérlegelésekor ügyeltünk arra, hogy ezek a kritériumok lehetővé tegyék a szabályozó paramétereinek meghatározását, ha adott a felépítése. Egy általánosabb probléma is felvethető: meg kell találni a szabályozási törvényt - egy analitikus függvényt, amely összeköti a vezérlési koordinátát és a vezérlési műveletet, miközben az integrált minőségi kritériumhoz min. A szabályozó differenciálegyenletének ilyen optimális kialakítását szabályozók analitikus tervezésének nevezzük. A megoldási módszerek és a probléma megfogalmazása szempontjából ez a probléma hasonló az optimális szabályozási problémákhoz.

Ez egy variációs probléma, ahol egy X-et és U-t összekötő függvényt keresünk szélsőértékként.

Az analitikai tervezésben egy olyan szabályozási törvény megtalálása a feladat, amely az üzemi egyenleteket és a peremfeltételeket figyelembe véve min a rendszer másodfokú hibáját jellemző integrálhoz szállítana, és garantálja annak stabilitását.

Szabályozók optimális tervezésének problémája.

A szabályozás tárgyát differenciálegyenletekkel adjuk meg, ami operátori formában megfelel a Wop(S) (vagy W(S)) átviteli függvény hozzárendelésének.

Úgy gondolják, hogy a külső perturbációk nem hatnak a rendszerre, és az átmeneti folyamat akkor következik be, amikor a kezdeti feltételek megváltoznak.

x = y 0 – y – eltérés

Egy stabil lineáris ACS-ben a tranziens folyamat eredményeként minden koordinátafüggvénynek 0-ra kell hajolnia. x 1 () = x 2 () = ... xn () = U () = 0 (2) )

Optimalitási kritériumként a forma integrálját választjuk

(3), ahol V egy pozitív határozott másodfokú forma.

Azok. ha V-t behelyettesítjük  (3)-ba, akkor ez lesz a rendszer másodfokú hibája.

A (4)-ben szereplő U 2 tag az ellenőrzési folyamat költségét jellemzi, azaz. fűtési energia költségek. Az U 2 garantálja a lineáris szabályozókban megvalósíthatatlan törvények hiányát, garantálja a szabályozási műveletek hiányát, amelyek mellett a sebesség végtelenné válik.

Maga a létezés (3) garantálja a rendszer stabilitását. Az analitikai tervezésben a feladat az Ф (U, U, x 1 ... xk) = 0 (5) függvény elemzési formában történő megtalálása - amely a növényegyenleteket és peremfeltételeket (1) és (2) figyelembe véve. ), minimális értéket adna az integrálhoz (3).

6.2.1. Problémák megfogalmazása és osztályozása az optimális szabályozás elméletében. Az általunk vizsgált problémák túlnyomó többségénél a vizsgált objektumok és rendszerek időbeli változásával összefüggő tényezőket kivettük a zárójelből. Talán, ha bizonyos előfeltételek teljesülnek, ez a megközelítés konstruktív és legitim. Az is világos azonban, hogy ez nem mindig elfogadható. Létezik egy kiterjedt problémaosztály, amelyben meg kell találni egy objektum optimális működését, figyelembe véve állapotainak időbeli és térbeli dinamikáját. Megoldásukra vonatkozó módszerek az optimális szabályozás matematikai elméletének tárgya.

Nagyon általános formában az optimális szabályozási probléma a következőképpen fogalmazható meg:

Van olyan objektum, amelynek állapotát kétféle paraméter jellemzi - állapotparaméterek és vezérlési paraméterek, és az utóbbi választásától függően az objektum kezelésének folyamata így vagy úgy halad. A vezérlési folyamat minőségét valamilyen funkcionális* segítségével értékeljük, amely alapján a feladat kijelölhető: meg kell találni a szabályozási paraméterek olyan értéksorát, amelyre ez a funkció szélső értéket vesz fel.

* funkcionalitás Egy numerikus függvényt hívunk meg, amelynek argumentumai általában más függvények.

Formális szempontból az optimális szabályozás számos problémája levezethető a nagy dimenziójú lineáris vagy nemlineáris programozás problémáira, mivel az állapottér minden pontja a saját ismeretlen változók vektorának felel meg. Ennek ellenére az ilyen irányú mozgás a megfelelő feladatok sajátosságainak figyelembevétele nélkül általában nem vezet racionális és hatékony megoldási algoritmusokhoz. Ezért az optimális szabályozási problémák megoldására szolgáló módszereket hagyományosan egy másik matematikai apparátushoz társítják, amely a variációszámításból és az integrálegyenletek elméletéből származik. Azt is meg kell jegyezni, hogy az optimális szabályozás elmélete – ismét történelmi okokból – a fizikai és műszaki alkalmazásokra fókuszált, és a gazdasági problémák megoldására való alkalmazása bizonyos értelemben másodlagos. Ugyanakkor számos esetben az optimális szabályozáselmélet apparátusát alkalmazó kutatási modellek is értelmes és érdekes eredményekhez vezethetnek.

A fent elmondottakhoz szükséges egy megjegyzést fűzni az optimális szabályozási problémák megoldására használt módszerek és a dinamikus programozás közötti szoros kapcsolathoz. Egyes esetekben alternatív alapon használhatók, míg más esetekben meglehetősen sikeresen kiegészítik egymást.

Különféle megközelítések léteznek az optimális szabályozási problémák osztályozására. Először is, a vezérlőobjektumtól függően osztályozhatók:

Ø Ø vezetési feladatokatösszevont paraméterek;

Ø Ø objektumkezelési feladatokat elosztott opciók.

Előbbire példa a repülőgép egészének irányítása, utóbbira pedig egy folyamatos technológiai folyamat irányítása.

Attól függően, hogy az alkalmazott kontrollok milyen eredményekhez vezetnek, vannak meghatározóés sztochasztikus feladatokat. Utóbbi esetben a kontrolleredmény olyan kimenetek halmaza, amelyeket bekövetkezésük valószínűsége ír le.

A szabályozott rendszer időbeli változásának természete szerint a feladatokat megkülönböztetjük:

Ø Ø diszkréttel változó idő;

Ø Ø s folyamatosan változó idő.

Hasonlóan osztályozzák a lehetséges állapotok diszkrét vagy folytonos halmazával rendelkező objektumok kezelésének problémáit. Azon rendszerek vezérlési feladatait, amelyekben az idő és az állapotok diszkréten változnak, vezérlési feladatoknak nevezzük. államgépek. Végül, bizonyos feltételek mellett problémák merülhetnek fel a vegyes rendszerek szabályozásában.

A vezérelt rendszerek számos modellje mind a közönséges, mind a parciális derivált differenciálegyenletek apparátusán alapul. Az elosztott paraméterű rendszerek vizsgálata során az alkalmazott parciális differenciálegyenletek típusától függően olyan optimális szabályozási problémákat különböztetünk meg, mint a parabola, az elliptikus vagy a hiperbolikus.

Vegyünk két legegyszerűbb példát a gazdasági objektumok kezelésének problémáira.

Erőforrás allokációs probléma. Elérhető T számokkal ellátott raktárak én (én∊1:m) homogén termék tárolására tervezték. Diszkrét időpontokban t∊0:(T-l) a fogyasztói tárgyak (kliensek) között számokkal oszlik meg j, j∊1:n. Raktárkészlet feltöltése a terméktároló helyeken ben t-adik időpillanatot a mennyiségek határozzák meg a i t,én∊1:m, és a benne lévő ügyfelek igényei egyenlőek b j t, j∊1:n. Jelölje c t i,j egységnyi termék kiszállításának költsége én raktár j-th fogyasztó időben t. Azt is feltételezik, hogy a termék, amely akkor érkezett a raktárba t, a következő pillanattól használható ( t+l). A megfogalmazott modellhez a feladat egy ilyen erőforrás-elosztási tervet találni ( x t i,j} Tm x n, amely minimalizálja a termékek raktárból történő kiszállításának összköltségét a rendszer teljes működése alatt.

Azon keresztül jelölve x t i,j szállított termék mennyisége j-th ügyfél én th raktárban t-adik időpontban és utána z t i- a termék teljes mennyisége én raktárban, a fent leírt probléma az ilyen változóhalmazok megtalálásának problémájaként ábrázolható

amelyek minimalizálják a funkciót

feltételek mellett

ahol a termék kezdeti készleteinek mennyiségei a raktárakban z 0 én = ž i. adottnak tételezzük fel.

A (6.20)-(6.23) feladatot hívjuk lineáris programozás dinamikus transzport problémája. A fenti terminológiát tekintve független változók x t i,j képviselni vezérlési paraméterek rendszer, és a tőlük függő változók z t i- összesített állapot paraméterei rendszerek bármikor. t. Korlátozások z t i≥ 0 garancia arra, hogy a tényleges mennyiségét meghaladó termékmennyiség bármikor nem exportálható egyetlen raktárból sem, és a (6.21) korlátozások határozzák meg ennek a mennyiségnek a megváltoztatásának szabályait az egyik időszakról a másikra való áttéréskor. Az ilyen típusú megszorításokat, amelyek feltételeket határoznak meg a rendszerállapot-paraméterek értékére, általában hívják fázis.

Azt is megjegyezzük, hogy a (6.21) feltétel a legegyszerűbb példa a fáziskényszerekre, mivel két szomszédos periódus állapotparamétereinek értékei összefüggenek. tés t+l. Általános esetben több, esetleg nem szomszédos szakaszhoz tartozó paramétercsoportra is megállapítható a függőség. Ilyen igény merülhet fel például, ha figyelembe vesszük a szállítási késedelem tényezőjét a modellekben.

A makroökonómia legegyszerűbb dinamikus modellje. Egy adott régió gazdaságát ábrázoljuk halmazként P iparágak ( j∊1:P), amelynek pénzben kifejezett bruttó terméke valamikor t vektorként ábrázolható z t=(z t 1 , z t 2 ,..., z t n), ahol t∊0:(T-egy). Jelölje Nál nél közvetlen költségmátrix, melynek elemei a t i,j tükrözik a termelési költségeket én-edik iparág (pénzben kifejezve) egy termelési egység előállítására j az iparban t-adik időpont. Ha X t= ║x t i,j║n x m- egy mátrix, amely meghatározza a termelés konkrét normáit én Az iparág bővíti a termelést j th iparág, és a t = (a t 1 , a t 2 , ..., a tn) a fogyasztásra használt fogyasztói szektorok termelési volumenének vektora, akkor a kiterjesztett szaporodás feltétele így írható fel.

ahol z 0 = ž - az iparágak kezdeti termékkínálatát adottnak és

A figyelembe vett modellben a mennyiségek z t rendszerállapot-paraméterek, és X t- szabályozási paraméterek. Ennek alapján különféle feladatok állíthatók fel, amelyeknek tipikus képviselője a gazdaság pillanatnyilag optimális kibocsátásának problémája T egy adott államhoz z*. Ez a probléma a vezérlési paraméterek sorozatának megtalálására redukálódik

feltételek teljesítése (6.24)-(6.25) és a funkció minimalizálása

6.2.2. A legegyszerűbb optimális szabályozási probléma. A szélsőséges problémák megoldásának egyik technikája az, hogy izolálunk néhány olyan problémát, amely viszonylag egyszerű megoldást enged meg, amelyre a jövőben más problémák is redukálhatók.

Tekintsük az ún a legegyszerűbb vezérlési probléma. Úgy néz ki mint

A (6.27)-(6.29) feladat feltételeinek sajátossága, hogy a szabályozási minőségfüggvények (6.27) és a megszorítások (6.28) lineárisak a z t, ugyanakkor a funkció g(t, x t) a (6.28)-ban tetszőleges lehet. Az utolsó tulajdonság nemlineárissá teszi a problémát még for t=1, vagyis a statikus változatban.

A (6.27)-(6.29) probléma megoldásának általános gondolata az egyes időpillanatokra vonatkozó részfeladatokra való "felosztásra" redukálódik, feltéve, hogy azok sikeresen megoldhatók. Szerkesszük meg a (6.27)-(6.29) feladatra a Lagrange függvényt

ahol λ t- Lagrange-szorzók vektora ( t∊0:T). Az általános jellegű megszorítások (6.29) ebben az esetben nem szerepelnek a (6.30) függvényben. Írjuk meg kicsit más formában

A Ф függvény szélsőértékének szükséges feltételei (x, z,λ) a vektorok halmazával z t az egyenletrendszer adja meg

amelyet úgy hívnak konjugált változók rendszere. Mint látható, a λ paraméterek megtalálásának folyamata t rendszerben (6.32) ismétlődően, fordított sorrendben hajtjuk végre.

A Lagrange-függvény extrémumának szükséges feltételei a λ változókban t ekvivalens lesz a (6.28) megszorításokkal, és végül a szélsőségének feltételeivel a vektorok halmazához képest x t∊X t, t∊1:(T-1) meg kell találni a probléma megoldásának eredményeként

Így az optimális szabályozás megtalálásának problémája olyan vezérlők megtalálására redukálódik, amelyek gyanakodnak az optimalitásra, azaz olyanokra, amelyekre a szükséges optimalitási feltétel teljesül. Ez viszont abból adódik, hogy ilyeneket találunk t, t, t, kielégítve a (6.28), (6.32), (6.33) feltételrendszert, amely ún. diszkrét Pontryagin maximum elv.

A tétel helyes.

Bizonyíték.

Hadd t, t, t, kielégíti a (6.28), (6.32), (6.33) rendszert. Ekkor (6.31) és (6.32) az következik, hogy

és azóta t kielégíti (6,33), akkor

Másrészt a (6.28) miatt (6.30)-ból az következik, hogy bármely vektorra t

Ennélfogva,

A (6.2) tételt, valamint a nemlineáris programozás elméletének egy extrém probléma megoldása és egy nyeregpont létezése közötti összefüggésre vonatkozó rendelkezéseit alkalmazva (lásd 2.2.2. fejezet) arra a következtetésre jutunk, hogy a vektorok t, t megoldást jelentenek a legegyszerűbb optimális szabályozási feladatra (6.27)-(6.29).

Ennek eredményeként egy logikailag egyszerű sémát kaptunk a probléma megoldására: a (6.32) relációk határozzák meg a konjugált változókat t, akkor a (6.33) feladat megoldása során megkeressük a vezérlőket tés távolabb (6.28) - az állapotok optimális pályája t,.

A javasolt módszer az optimális szabályozás elméletének alapvető eredményei közé tartozik, és, mint fentebb említettük, számos bonyolultabb probléma megoldásához fontos, amelyek így vagy úgy, a legegyszerűbbre redukálódnak. Ugyanakkor nyilvánvalóak a hatékony felhasználás korlátai is, amelyek teljes mértékben a (6.33) probléma megoldási lehetőségétől függenek.

KULCSFOGALMAK

Ø Ø Játék, játékos, stratégia.

Ø Ø Zéró összegű játékok.

Ø Ø Mátrix játékok.

Ø Ø Antagonisztikus játékok.

Ø Ø Maximum és minimax alapelvei.

Ø Ø A játék nyeregpontja.

Ø Ø A játék ára.

Ø Ø Vegyes stratégia.

Ø Ø Mátrixjátékok főtétele.

Ø Ø Dinamikus szállítási probléma.

Ø Ø A makroökonómia legegyszerűbb dinamikus modellje.

Ø Ø A legegyszerűbb optimális szabályozási probléma.

Ø Ø Diszkrét Pontryagin maximum elv.

ELLENŐRZŐ KÉRDÉSEK

6.1. Fogalmazza meg röviden a játékelmélet, mint tudományos diszciplína tárgyát.

6.2. Mit jelent a "játék" szó?

6.3. Milyen gazdasági helyzetek leírására alkalmazható a játékelméleti apparátus?

6.4. Mi az antagonisztikus játék?

6.5. Mi határozza meg egyedileg a mátrixjátékokat?

6.6. Mi a maximin és a minimax alapelve?

6.7. Milyen feltételek mellett mondhatjuk, hogy a játéknak van nyeregpontja?

6.8. Mondjon példákat olyan játékokra, amelyeknek van és nincs nyereghegye!

6.9. Milyen módszerek léteznek az optimális stratégiák meghatározására?

6.10. Mit nevezünk „játék árának”?

6.11. Határozza meg a „vegyes stratégia” fogalmát.

BIBLIOGRÁFIA

1. Abramov L. M., Kapustin V. F. Matematikai programozás. L., 1981.

2. Ashmanov S.A. Lineáris programozás: Proc. juttatás. M., 1981.

3. Ashmanov S. A., Tikhonov A. V. Optimalizálás elmélete feladatokban és gyakorlatokban. M., 1991.

4. Bellman R. Dinamikus programozás. M., 1960.

5. Bellman R., Dreyfuss S. A dinamikus programozás alkalmazott problémái. M., 1965.

6. Gavurin M. K., Malozemov V. N. Extrém problémák a lineáris kényszerekkel. L., 1984.

7. Gass S. Lineáris programozás (módszerek és alkalmazások). M., 1961.

8. Gale D. Lineáris gazdasági modellek elmélete M., 1963.

9. Gill F., Murray W., Wright M. Gyakorlati optimalizálás / Per. angolról. M., 1985.

10. Davydov E. G. Operations Research: Proc. egyetemi hallgatók támogatása. M., 1990.

11. Danzig J. Lineáris programozás, általánosításai és alkalmazásai. M., 1966.

12. Eremin I. I., Asztafjev N. N. Bevezetés a lineáris és konvex programozás elméletébe. M., 1976.

13. Ermoliev Yu.M., Lyashko I.I., Mikhalevich V.S., Tyuptya V.I. A műveletek kutatásának matematikai módszerei: Proc. juttatás az egyetemek számára. Kijev, 1979.

14. Zaichenko Y.P. Operations Research, 2. kiadás. Kijev, 1979.

15. Zangwill W.I. Nemlineáris programozás. Egységes megközelítés. M., 1973.

16. Zeutendijk G. A lehetséges irányok módszerei. M., 1963.

17. Karlin S. Matematikai módszerek játékelméletben, programozásban és közgazdaságtanban. M., 1964.

18. Karmanov V. G. Matematikai programozás: Proc. juttatás. M., 1986.

19. Korbut A.A., Finkelyitein Yu. Yu. Diszkrét programozás. M., 1968.

20. Kofman A., Henri-Laborder A. A műveletek kutatásának módszerei és modelljei. M., 1977.

21. Künze G.P., Crelle V. Nemlineáris programozás. M., 1965.

22. Lyashenko I.N., Karagodova E.A., Chernikova N.V., Shor N.3. Lineáris és nemlineáris programozás. Kijev, 1975.

23. McKinsey J. Bevezetés a játékelméletbe. M., 1960.

24. Mukhacheva E. A., Rubinstein G. Sh. Matematikai programozás. Novoszibirszk, 1977.

25. Neumann J., Morgenstern O. Játékelmélet és gazdasági magatartás. M, 1970.

26. Ore O. Gráfelmélet. M., 1968.

27. Taha X. Bevezetés az operációkutatásba / Per. angolról. M., 1985.

28. Fiakko A., McCormick G. Nemlineáris programozás. A szekvenciális feltétel nélküli minimalizálás módszerei. M., 1972.

29. Hadley J. Nemlineáris és dinamikus programozás. M., 1967.

30. Yudin D.B., Holstein E.G. Lineáris programozás (elmélet, módszerek és alkalmazások). M., 1969.

31. Yudin D.B., Holstein E.G. Lineáris programozás. Elmélet és véges módszerek. M., 1963.

32. Lapin L. Kvantitatív módszerek ügyes üzleti döntésekhez. Negyedik kiadás. HBJ, 1988.

33. Liitle I.D.C., Murty K.G., Sweeney D.W., Karel C. Utazási algoritmus az utazó eladó problémájára. - Operation Research, 1963, 11. évf. 6. o. 972-989/ Orosz. ford.: Little J., Murthy K., Sweeney D., Kerel K. Algoritmus az utazó eladó probléma megoldására. - A könyvben: Economics and Mathematical Methods, 1965, 1. évf., 1. sz., p. 94-107.

ELŐSZÓ ................................................. .............................................................. ............................................................ ...................................................... ...................... 2

BEVEZETÉS ................................................... ................................................... .................................................. ................................................ .. ........ 3

1. FEJEZET LINEÁRIS PROGRAMOZÁS ................................................... .................................................. ................................................................ ......... nyolc

1.1. A LINEÁRIS PROGRAMOZÁS FELADATÁNAK MEGFOGALMAZÁSA ................................................... ................................................................ ................ 9

1.2. A ZLP FŐ TULAJDONSÁGAI ÉS ELSŐ GEOMETRIAI ÉRTELMEZÉSE................................................ .................................................................. tizenegy

1.3. ALAPVETŐ MEGOLDÁSOK ÉS A ZLP MÁSODIK GEOMETRIAI ÉRTELMEZÉSE................................................ .................................................................. ...... 15

1.4. EGYSZERŰ MÓDSZER................................................ .................................................. ................................................ .. ...................................... 17

1.5. MÓDOSÍTOTT SIMPLEX MÓDSZER................................................ ................................................................ ................................................................ ......... 26

1.6. DUALITÁS ELMÉLET A LINEÁRIS PROGRAMOZÁSBAN................................................ ................................................................ ............................. harminc

1.7. KETTŐS EGYSZERŰ MÓDSZER.................................................. ................................................................ ................................................................ .................. .37

KULCSFOGALMAK................................................ ............................................................ .............................................................. .............................................................. 42

ELLENŐRZŐ KÉRDÉSEK................................................ .................................................. ................................................ .. .............................. 43

2. FEJEZET NEMLINEÁRIS PROGRAMOZÁS ................................................... .............................................................. .............................................................. ... 44

2.1. MÓDSZEREK A NEMLINEÁRIS PROGRAMOZÁSI PROBLÉMÁK MEGOLDÁSÁRA................................................ ................................................................ .............................. 44

2.2. DUALITÁS A NEMLINEÁRIS PROGRAMOZÁSBAN................................................ .................................................. ................................... ... 55

FEJEZET 3. SZÁLLÍTÁSI ÉS HÁLÓZATI FELADATOK ............................................ ................................................................ ................................................................ ... 60

3.1. SZÁLLÍTÁSI PROBLÉMA ÉS MEGOLDÁSÁNAK MÓDSZEREI ................................................... ................................................................ .............................................. 60

3.2. HÁLÓZATI FELADATOK................................................ ................................................................ .................................................. ................................................................ .............. 66

4. FEJEZET DISZKRÉT PROGRAMOZÁS ................................................. .................................................. ................................................................ .. 74

4.1. A DISZKRÉT PROGRAMOZÁSI FELADATOK TÍPUSAI................................................ ................................................................ .................................................. ..... 74

4.2. GOMORY MÓDSZER................................................ .. .................................................. ................................................... ................................................ 78

4.3. ELÁGAZÁSI ÉS KÖTÉSI MÓDSZER................................................... ...................................................... ...................................................... .......................................... 81

5. FEJEZET DINAMIKUS PROGRAMOZÁS ................................................... .................................................. .............................................. 86

5.1. A DINAMIKUS PROGRAMOZÁSI MÓDSZEREK ÁLTALÁNOS VÁZMA................................................ ................................................................ ........................ 86

5.2. PÉLDÁK DINAMIKUS PROGRAMOZÁSI FELADATOKRA................................................ ................................................................ ................................................ 93

6. FEJEZET A MŰKÖDÉSI TANULMÁNY EGYÉB RÉSZEINEK ÁTTEKINTÉSE................................................ .............................................. 101

6.1. JÁTÉKELMÉLET................................................ .................................................. ................................................ .. ................................................ 101

6.2. OPTIMÁLIS SZABÁLYOZÁS ELMÉLETE................................................ ................................................................ .................................................................. .......................... 108

BIBLIOGRÁFIA................................................ . ................................................ .. ................................................................ ................................ 112

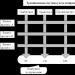
Bármilyen automata rendszert valamilyen objektum vezérlésére terveztek, úgy kell felépíteni, hogy a vezérlése optimális legyen, vagyis ilyen vagy olyan értelemben a legjobb legyen. Az optimális szabályozási problémák leggyakrabban a folyamatirányítási alrendszerekben merülnek fel. Minden esetben van egy bizonyos technológiai feladat, amelyre a megfelelő gépet vagy berendezést (vezérlő objektumot) szánják, felszerelve a megfelelő vezérlőrendszerrel, pl. néhány ACS-ről beszélünk, amely egy vezérlőobjektumból és egy sor eszközből áll, amelyek biztosítják az objektum vezérlését. Ez a készlet általában mérő-, erősítő átalakító és működtető eszközöket tartalmaz. Ha az erősítő, átalakító és működtető eszközöket egyetlen linkben, úgynevezett vezérlőkészülékben vagy szabályozóban kombinálja, akkor az ACS működési diagramja a 2. ábrán látható formába hozható. tizenegy.

Rizs. 12 Az optimális rendszer funkcionális diagramja

A vezérlőeszköz bemenete egy beállítási műveletet kap, amely utasításokat tartalmaz arra vonatkozóan, hogy milyen állapotban kell lennie az objektumnak - az úgynevezett "kívánt állapotnak".

A vezérlőobjektum z zavaró műveletet kaphat, amely terhelést vagy interferenciát jelent. Egy objektum koordinátáinak mérőeszközzel történő mérése néhány véletlenszerű hibával x (hiba) végezhető.

A vezérlőberendezés feladata tehát egy olyan vezérlési művelet kidolgozása, hogy az ACS egészében működő minősége bizonyos értelemben a legjobb legyen. A vezérlőberendezés algoritmusának meghatározásához ismerni kell az objektum jellemzőit, valamint az objektumról és a zavarokról érkező információ természetét, amely a vezérlőkészülékbe kerül.

Az objektum jellemzői alatt érthető az objektum kimeneti értékeinek a bemenettől való függése

ahol F általában egy operátor, amely megfelelési törvényt hoz létre két függvénykészlet között. Egy objektum F operátora többféleképpen adható meg: képletek, táblázatok, grafikonok segítségével. Be van állítva egy differenciálegyenlet-rendszer formájában is, amely vektor formában így van felírva

ahol és megadták a vektor kezdeti és végső értékét.

A vizsgált probléma megoldásának számos különböző módja van. De egy objektum kezelésének csak egy módja adja a legjobb eredményt bizonyos értelemben. Ezt a szabályozási módot és az azt megvalósító rendszert optimálisnak nevezzük.

Ahhoz, hogy kvantitatív okunk legyen az egyik szabályozási mód előnyben részesítésére másokkal szemben, meg kell határozni az ellenőrzési célt, majd be kell vezetni egy, a cél elérésének hatékonyságát jellemző mérőszámot - az ellenőrzési optimalitás kritériumát. Általában az optimalitási kritérium egy olyan számérték, amely a rendszer időben és térben változó koordinátáitól és paramétereitől függ, így a kritérium egy bizonyos értéke megfelel az egyes szabályozási törvényeknek. Optimalitási kritériumként a vizsgált folyamat különféle műszaki és gazdasági mutatói választhatók.

Néha eltérő, néha egymásnak ellentmondó követelményeket támasztanak az irányítási rendszerrel szemben. Nincsenek olyan szabályozási törvények, amelyek az egyes követelményeket egyidejűleg a legjobban kielégítenék. Ezért az összes követelmény közül ki kell választania egy fő követelményt, amelyet a legjobb módon kell kielégíteni. Más követelmények játsszák a megszorítások szerepét. Ezért az optimalitási kritérium kiválasztását csak a vizsgált objektum és környezet technológiájának és gazdaságosságának tanulmányozása alapján szabad meghozni. Ez a feladat túlmutat az op-erősítők elméletén.

Az optimális szabályozási feladatok megoldása során a legfontosabb az irányítás céljának kitűzése, amely matematikailag egy bizonyos Q értékű szélsőség elérésének problémájaként fogható fel - az optimalitási kritérium. A matematikában az ilyen mennyiséget funkcionálisnak nevezik. A megoldandó problémától függően minimális vagy maximum Q elérése szükséges. Például írunk egy optimalitási feltételt, amelyben Q minimális legyen.

Mint látható, Q értéke függ a függvényektől.

Optimalitási kritériumként különféle műszaki és műszaki-gazdasági mutatók, becslések vehetők fel. Az optimalitási kritérium megválasztása mérnöki és mérnök-gazdasági feladat, amelyet a szabályozott folyamat mélyreható és átfogó vizsgálata alapján oldanak meg. Az irányításelméletben széles körben használják az integrál funkcionálisokat, amelyek a rendszer működésének minőségét jellemzik. Ennek a funkciónak a maximális vagy minimális értékének elérése jelzi a rendszer optimális viselkedését vagy állapotát. Az integrált funkciók általában tükrözik a vezérlőobjektumok működési feltételeit, és figyelembe veszik a koordinátákra szabott korlátozásokat (fűtésre, erősségre, energiaforrások teljesítményére stb.).

Az irányítási folyamatokhoz a következő kritériumokat alkalmazzák:

1. optimális teljesítmény (tranziens idő)

2. minimális négyzetes hiba.

3. minimális energiafogyasztás.

Így az optimalitási kritérium utalhat egy átmeneti vagy állandó folyamatra a rendszerben.

Az optimalitási kritériumtól függően az optimális rendszerek két fő osztályba sorolhatók - optimális sebességre és optimális pontosságra.

Az optimális vezérlőrendszerek az optimalitási kritérium jellegétől függően három típusra oszthatók:

a) egységesen optimális rendszerek;

b) statisztikailag optimális rendszerek;

c) minimax-optimális rendszerek.

Az egységesen optimális rendszer az, amelyben minden egyes folyamat optimális. Például a sebesség-optimális rendszerekben bármilyen kezdeti körülmény és bármilyen zavarás esetén a rendszer a legrövidebb időn keresztül jut el a kívánt állapotba.

A statisztikailag optimális rendszerekben az optimalitási kritérium statisztikai jellegű. Az ilyen rendszereknek átlagosan a legjobbaknak kell lenniük. Itt az egyes folyamatok optimalizálása nem szükséges vagy lehetetlen. Statisztikai kritériumként leggyakrabban egy elsődleges kritérium átlagértéke jelenik meg, például egy bizonyos határon túlmutató érték matematikai elvárása.

A Minimax-optimális rendszerek olyan rendszerek, amelyek a legrosszabb esetben a lehető legjobb eredményt adják. Az egységesen optimálisaktól abban különböznek, hogy nem legrosszabb esetben rosszabb eredményt tudnak adni, mint bármely más rendszer.

Az optimális rendszerek három típusra oszthatók a kezelt objektumról való információszerzés módjától függően:

optimális rendszerek teljes információval az objektumról;

optimális rendszerek hiányos információkkal az objektumról és annak passzív felhalmozódásáról;

optimális rendszerek hiányos információkkal az objektumról és annak aktív felhalmozódásáról a vezérlési folyamatban (kettős vezérlési rendszerek).

Kétféle optimális rendszerszintézis probléma létezik:

A vezérlő paramétereinek optimális értékeinek meghatározása az objektum adott paramétereihez és a rendszer adott struktúrájához;

A vezérlő szerkezetének szintézise és paramétereinek meghatározása adott paraméterekhez és a vezérlőobjektum szerkezetéhez.

Az első típusú problémák megoldása különböző analitikai módszerekkel, az integrálbecslések minimalizálása mellett, valamint számítástechnika (számítógépes modellezés) segítségével, adott optimalitási feltétel figyelembevételével lehetséges.

A második típusú feladatok megoldása speciális módszerek alkalmazásán alapul: a klasszikus variációs számítás módszerei, a Pontryagin-féle maximumelv és a Bellman-féle dinamikus programozás, valamint a matematikai programozás módszerei. Az optimális rendszerek véletlenszerű jelekkel történő szintéziséhez Wiener-módszereket, variációs és frekvenciamódszereket alkalmaznak. Az adaptív rendszerek fejlesztésében a legszélesebb körben alkalmazott gradiens módszerek, amelyek lehetővé teszik a törvények, az állítható paraméterek változásainak meghatározását.

Az elmúlt években az optimális szabályozást mind a műszaki rendszerekben alkalmazták a termelési folyamatok hatékonyságának javítására, mind a szervezetirányítási rendszerekben a vállalkozások, szervezetek, nemzetgazdasági ágazatok tevékenységének javítására.

A szervezeti rendszerekben gyakori, hogy megvizsgálás nélkül érdeklődnek a csapat végjátékának eredménye iránt

hatékonyság a parancs kiadása és a végeredmény megszerzése közötti átmeneti folyamat során.Ez azzal magyarázható, hogy általában az ilyen rendszerekben a tranziens folyamat veszteségei meglehetősen kicsik, és nem befolyásolják jelentősen a teljes nyereséget állandósult állapotban, mivel a maga az egyensúlyi állapot sokkal hosszabb, mint az átmeneti folyamat. De néha matematikai nehézségek miatt nem fedezik fel a dinamikát. Módszertanfolyamok a szervezeti és gazdasági rendszerek végső állapotának optimalizálásának módszerei. optimalizálás és műveletek kutatása.

A dinamikus műszaki rendszerek vezérlésében az optimalizálás gyakran éppen az átmeneti folyamatoknál elengedhetetlen, ahol a hatékonysági mutató nemcsak a koordináták aktuális értékétől függ (mint az extrém szabályozásnál), hanem a változás jellegétől is. a múlt, a jelen és a jövő, és a koordinátákon, azok származékain és esetleg az időn valamilyen funkcionális kifejeződik.

Példa erre egy sportoló távoli futásának menedzselése. Mivel energiatartalékát élettani tényezők korlátozzák, és a tartalék felhasználása a futás jellegétől függ, a sportoló már nem tudja minden pillanatban a lehető legnagyobb erőt adni, hogy ne használja fel idő előtt az energiatartalékát és ne futjon. távolról gőzerőből, de meg kell keresnie az adottságainak megfelelő optimális futási módot.

Az ilyen dinamikus problémákban az optimális szabályozás megtalálásához a rendszer matematikai leírásának (matematikai modelljének) típusától függően a vezérlési folyamatban egy meglehetősen összetett matematikai probléma megoldására van szükség variációszámítási módszerekkel vagy matematikai programozással. Így egy számítástechnikai eszköz vagy számítógép az optimális vezérlőrendszer szerves részévé válik. Az elvet a ábra szemlélteti. 1.10. A VM számítási eszközének (gépének) bemenete információkat kap az x koordináták aktuális értékeiről az O objektum kimenetéről, a vezérlőkről és a bemenetéről, az objektumra gyakorolt z külső hatásokról, valamint különböző feltételek meghatározása kívülről: a peremfeltételek optimálissági kritériumának értéke információ a megengedett értékekről Számítási

Állami oktatási intézmény

felsőfokú szakmai végzettség

Moszkvai Fizikai és Technológiai Intézet

(Állami Egyetem)

JÓVÁHAGY

tudományos rektorhelyettes

Yu.A.Samarsky

"________" _______________ 2004

PROGRAM

a tanfolyamon: OPTIMUM CONTROL

az 511600-as irányba

A FUPM Kar

Matematikai Irányítási Alapok Tanszék

jól IV

félév 7, 8

előadások - 50 óra. Vizsga - 8 félév

szemináriumok - 50 óra. Kredit - 7. félév

laborok - nem

Önálló munkavégzés - heti 2 óra

ÖSSZESEN 100 ÓRA

A programot és a feladatot összeállította: a fizikai és matematikai tudományok doktora, Zhadan V.G. professzor.

osztályvezető S.A. Liba

1. Az optimális szabályozás fő problémája. L.S. maximum elv Pontryagin (minimum elve). Kanonikus jelölés. A szabályozási paramétereket tartalmazó rendszerek maximális elve.

2. Problémák a mozgatható jobb véggel. transzverzalitási feltételek. Lagrange és Bolz problémái. Mayer és Lagrange problémák a nem rögzített folyamatleállítási idővel. Gyorsasági feladat. Probléma a mozgatható bal végével.

3. A maximum elv bizonyítása L.S. Pontryagin a Mayer-probléma miatt. A tűvariáció fogalma. Gronwall–Bellman lemma. Az optimalizálás elszámolása szabályozási paraméter szerint.

4. Maximum elv kapcsolata a variációszámítással. Euler egyenlet. Az Euler-egyenlet első integráljai. Weerstrass, Legendre és Jacobi körülményei. Jacobi egyenlet. Weerstrass–Erdmann feltételek.

5. Lineáris rendszerek. A lineáris rendszerek maximális elve. Tétel véges számú kapcsolási pontról.

6. Elérhetőségi készlet lineáris rendszerekhez. Extrém kontroll és extrém elv.

7. Pontszabályozhatóság lineáris rendszerek esetén. A pont irányíthatóság kritériuma. Kálmán-tétel a pontszabályozhatóságról. Lineáris rendszerek teljes irányíthatósága. Kálmán tétele az autonóm rendszerek teljes irányíthatóságáról.

8. A megfigyelhetőség problémája. Lineáris rendszer megfigyelhetőségi kritériuma. A kezdeti állapot megfigyelése. A megfigyelhetőség és az irányíthatóság kapcsolata. Stacionárius rendszer teljes megfigyelhetőségének kritériuma.

9. Lagrange formalizmus és felhasználása az optimális szabályozási problémák megoldására. Az optimális szabályozási szintézis problémája.

10. Az azonosítás problémája. Azonosítási kritérium. A helyhez kötött rendszer teljes azonosíthatóságának kritériuma.

11. Nem folytonos jobb oldali rendszerek. Ugrás feltétele.

12. Az invariáns rendszerek fogalma. Dinamikus rendszerek tulajdonságai. Az impulzusok referenciamezője. A változatlanság szükséges és elégséges feltételei. korrekciós funkció.

13. Elegendő feltételek az optimalitáshoz. A szélsőségek mezeje. Kapcsolódás elegendő Weerstrass-feltétellel a variációszámítás klasszikus problémájához.

14. A dinamikus programozás elméletének elemei. Az optimálissághoz szükséges feltételek. Elegendő optimalitási feltételek. Bellman egyenlet. A maximum elv levezetése dinamikus programozásból. Kapcsolódás a variációszámításhoz.

15. A határérték-feladatok megoldásának módszerei. Newton-módszer alkalmazása. Peremfeltételek átadása. Sweep módszer nemlineáris problémákhoz.

16. Változatok szekvenciális elemzésén alapuló numerikus módszerek. A kijevi seprű módszer, a vándorcső módszer, a helyi variációk módszere.

17. Nemlineáris programozási feladatokra való redukción alapuló numerikus módszerek. A vezérlővektor összetevőire vonatkozó deriváltak számítása diszkrét folyamatok esetén. Büntetésmódszer, betöltött funkcionális módszer.

18. Diszkrét minimum elv. Variációs egyenlőtlenségek. A feltételes gradiens módszer alkalmazása optimális szabályozási problémák megoldására. A kvázi-minimum elve.

19. Elegendő optimalitási feltételek V.F. Krotov folyamatos és diszkrét folyamatokhoz. Alkalmazása V.F. Krotov a lineáris feladatok megoldására.

20. Különleges kezelőszervek. Speciális vezérlések meghatározása Poisson zárójelek segítségével. Kelly és Kopp-Moyer állapotok.

BIBLIOGRÁFIA

1. Moiseev N.N. Numerikus módszerek az optimális rendszerek elméletében. – M.: Nauka, 1971.

2. Jevtusenko Yu.G. Extrém problémák megoldásának módszerei és alkalmazása optimalizáló rendszerekben. – M.: Nauka, 1982.

3. Moiseev N.N., Ivanilov Yu.P., Stolyarova E.M. Optimalizálási módszerek. – M.: Nauka, 1987.

4. Pontryagin L.S., Boltyansky V.G., Gamkrelidze Z.V., Mishchenko E.F. Optimális folyamatok matematikai elmélete. – M.: Fizmatgiz, 1961.

5. Vasziljev F.P. Extrém problémák megoldásának módszerei. – M.: Nauka, 1988.

6. Gabasov R., Kirillova F.M. A maximum elv az optimális szabályozás elméletében. - Minszk: Tudomány és technológia, 1974.

7. Fleming W., Richel R. Determinisztikus és sztochasztikus rendszerek optimális szabályozása. – M.: Mir, 1978.

8. Az optimális szabályozás elméletének alapjai /Szerk V F. Krotov.- M .: Felsőiskola, 1990.

9. Lee E.B., Marcus P. Az optimális szabályozás elméletének alapjai. Moszkva: Nauka, 1972.

10. Gabasov R., Kirillova F.M. Speciális optimális vezérlések. – M.: Nauka, 1973.

A feladat megtekinthető

Optimális automata vezérlőrendszerek osztályozása Angol tudósok munkarendszereinek optimális vezérlése

A cég stratégiai irányítása Stratégiai irányítási rendszer

Optimális automata vezérlőrendszerek. Optimális automata vezérlőrendszerek osztályozása Angol tudósok munkarendszereinek optimális vezérlése

28. Szabályozók analitikai tervezése. A probléma megfogalmazása.

PROGRAM

Kategóriák

Népszerű bejegyzések

Legutóbbi bejegyzések